主成分分析の2種類の定式化 – Diversity Mining Laboratory @ Rikkyo University

$D$ 次元空間に $N$ 個のベクトル $\boldsymbol{x}_1,\ldots,\boldsymbol{x}_N$ があるとする。
平均は原点に一致するとする。つまり、 $\frac{1}{N}\sum_{n=1}^N \boldsymbol{x}_n = \boldsymbol{0}$ と仮定する。
各ベクトルのエントリは、 $\boldsymbol{x}_n = (x_{n1},\ldots,x_{nD})^T$ と書くことにする。

さて、これらの $N$ 個のベクトルの集合に対して、
ある単位ベクトル $\boldsymbol{u}$ をとって、下記の2種類のいずれかの条件を満たすようにする。
2種類の条件とは、分散の最大化と、残差平方和の最小化である。

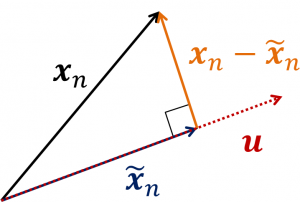
分散の最大化で考える分散とは、 $N$ 個のベクトル $\boldsymbol{x}_n$ を
$\boldsymbol{u}$ へ正射影したベクトル $\tilde{\boldsymbol{x}}_n$ の長さの分散である。

残差平方和の最小化で考える残差とは、
正射影したベクトル $\tilde{\boldsymbol{x}}_n$ と元のベクトル $\boldsymbol{x}_n$ との差ベクトルの長さである。

2種類の条件のどちらを考えても、全く同じ $\boldsymbol{u}$ が答えとして求まる、
というのが、この記事で言いたいことである。

１．分散を最大化する

ベクトル $\boldsymbol{u}$ の上に $N$ 個のベクトルそれぞれを正射影する。
ということは、各 $\boldsymbol{x}_n$ について、 $\boldsymbol{u}^T (\boldsymbol{x}_n - \tilde{\boldsymbol{x}}_n) = 0$ かつ $\tilde{\boldsymbol{x}}_n = t \boldsymbol{u}$ を満たす $\tilde{\boldsymbol{x}}_n$ を求めればよい。

$\boldsymbol{u}^T (\boldsymbol{x}_n - t \boldsymbol{u}) = 0$ を解くと、 $\boldsymbol{u}^T \boldsymbol{x}_n - t \boldsymbol{u}^T \boldsymbol{u} = 0$ だから、 $t = \frac{\boldsymbol{u}^T \boldsymbol{x}_n}{\boldsymbol{u}^T \boldsymbol{u}}$ を得る。
$\boldsymbol{u}$ は単位ベクトルだったから、 $\boldsymbol{u}^T \boldsymbol{u}$ 。
よって、 $t = \boldsymbol{u}^T \boldsymbol{x}_n$ である。

つまり、 $\boldsymbol{u}$ の上に、各ベクトル $\boldsymbol{x}_n$ を正射影すると、 $(\boldsymbol{u}^T \boldsymbol{x}_n) \boldsymbol{u}$ というベクトルを得る。
これら正射影ベクトルの長さ $\boldsymbol{u}^T \boldsymbol{x}_n$ の分散

$\frac{1}{N}\sum_{n=1}^N (\boldsymbol{u}^T \boldsymbol{x}_n)^2$
を最大化する $\boldsymbol{u}$ を求めてみる。（ $N$ でなく $N-1$ で割っても答えは同じ。）

$\boldsymbol{u}$ は単位ベクトルなので、 $\boldsymbol{u}^T\boldsymbol{u}=1$ を満たさなければならない。
そこで、ラグランジュの未定乗数法を使い、

$L(\boldsymbol{u}) = \frac{1}{N}\sum_n (\boldsymbol{u}^T \boldsymbol{x}_n)^2 + \lambda (1 - \boldsymbol{u}^T\boldsymbol{u})$
を最大化する。
そのためには、 $\frac{\partial L(\boldsymbol{u})}{\partial u_{d}}$ を各 $d$ について求め、 $\frac{\partial L(\boldsymbol{u})}{\partial u_{d}} = 0$ を解けばよい。

偏微分を計算する前に、 $L(\boldsymbol{u})$ の各項を細かく書き下す。

$L(\boldsymbol{u}) = \frac{1}{N}\sum_n (\sum_d u_d x_{nd})^2 + \lambda (1 - \sum_d u_d^2)$
さらに細かく書き下す。
$L(\boldsymbol{u}) = \frac{1}{N}\sum_n (\sum_d u_d^2 x_{nd}^2 + 2 \sum_d \sum_{d^\prime \neq d} u_d u_{d^\prime} x_{nd}x_{nd^\prime}) + \lambda (1 - \sum_d u_d^2)$
よって、
$\frac{\partial L(\boldsymbol{u})}{\partial u_{d}} = \frac{1}{N}\sum_n \{2 x_{nd}^2 u_d + 2 \sum_{d^\prime \neq d} (x_{nd} x_{nd^\prime}) u_{d^\prime} \} - 2 \lambda u_d$
を得る。 $\frac{\partial L(\boldsymbol{u})}{\partial u_{d}} = 0$ とおくと、
$\frac{1}{N}\sum_n \{ x_{nd}^2 u_d + \sum_{d^\prime \neq d} (x_{nd} x_{nd^\prime}) u_{d^\prime} \} = \lambda u_d$
を解けばよいことが分かる。

左辺は、次のように書き直せる。

$(\frac{1}{N}\sum_n x_{nd}^2) u_d + \sum_{d^\prime \neq d} (\frac{1}{N}\sum_n x_{nd} x_{nd^\prime}) u_{d^\prime} = \lambda u_d$
よく見ると、 $(\frac{1}{N}\sum_n x_{nd}^2)$ はベクトルの $d$ 番目のエントリに関する分散で、
$(\frac{1}{N}\sum_n x_{nd} x_{nd^\prime})$ はベクトルの $d$ 番目と $d^\prime$ 番目のエントリに関する共分散になっている。

そこで、 $\boldsymbol{x}_1,\ldots,\boldsymbol{x}_N$ の分散共分散行列 $\boldsymbol{S}$ を使って、さらに書き直す。

$\boldsymbol{S}_{dd} u_d + \sum_{d^\prime \neq d} \boldsymbol{S}_{dd^\prime} u_{d^\prime} = \lambda u_d$
なお、 $\boldsymbol{S}_{dd^\prime}$ は、行列 $\boldsymbol{S}$ の第 $d$ 行第 $d^\prime$ 列の成分のことである。

行列 $\boldsymbol{S}$ の第 $d$ 行を $\boldsymbol{S}_d$ と書くことにすると、
これはさらに、下のように書き直せる。

$\boldsymbol{S}_d^T \boldsymbol{u} = \lambda u_d$

$d=1,\ldots,D$ すべてについて結果をまとめて書くと

$\boldsymbol{S} \boldsymbol{u} = \lambda \boldsymbol{u}$
となる。つまり、 $\boldsymbol{u}$ はこの方程式を満たす。

ここで、最大化したかった分散を思い出す。

$\frac{1}{N}\sum_{n=1}^N (\boldsymbol{u}^T \boldsymbol{x}_n)^2$
先ほどの方程式 $\boldsymbol{S} \boldsymbol{u} = \lambda \boldsymbol{u}$ を満たす $\boldsymbol{u}$ については、
この分散の値はどのように書き直せるだろうか。

この分散を、細かく書き下してみると

$\frac{1}{N}\sum_{n=1}^N (\boldsymbol{u}^T \boldsymbol{x}_n)^2 = \frac{1}{N}\sum_n (\sum_d u_d x_{nd})^2$
となる。その一方、 $\frac{\partial L(\boldsymbol{u})}{\partial u_{d}} = 0$ とおくことで、
$\frac{1}{N}\sum_n \{ x_{nd}^2 u_d + \sum_{d^\prime \neq d} (x_{nd} x_{nd^\prime}) u_{d^\prime} \} = \lambda u_d$
つまり
$\frac{1}{N}\sum_n \sum_{d^\prime=1}^D (x_{nd} x_{nd^\prime}) u_{d^\prime} = \lambda u_d$
を得ていた。左辺が分散の式と似ている。そこで、この両辺に $u_d$ を掛けてみる。
$\frac{1}{N}\sum_n \sum_{d^\prime=1}^D (x_{nd} u_d) (x_{nd^\prime} u_{d^\prime}) = \lambda u_d^2$
両辺の $d$ についての和を求める。
$\frac{1}{N}\sum_n \sum_{d=1}^D \sum_{d^\prime=1}^D (x_{nd} u_d) (x_{nd^\prime} u_{d^\prime}) = \lambda \sum_{d=1}^D u_d^2$
よく見ると、左辺は分散 $\frac{1}{N}\sum_{n=1}^N (\boldsymbol{u}^T \boldsymbol{x}_n)^2$ と全く同じ式になっている。
右辺は $\boldsymbol{u}$ が単位ベクトルであることより $\lambda$ に等しい。
つまり、
$\frac{1}{N}\sum_{n=1}^N (\boldsymbol{u}^T \boldsymbol{x}_n)^2 = \lambda$
という関係式を得た。 $\lambda$ は分散に等しくなるのである。

同じことは、分散の式を次のように変形しても導ける。

$\frac{1}{N}\sum_{n=1}^N (\boldsymbol{u}^T \boldsymbol{x}_n)^2 = \frac{1}{N}\sum_{n=1}^N (\boldsymbol{u}^T \boldsymbol{x}_n)(\boldsymbol{x}_n^T \boldsymbol{u}) = \frac{1}{N}\sum_{n=1}^N \boldsymbol{u}^T (\boldsymbol{x}_n \boldsymbol{x}_n^T) \boldsymbol{u} = \boldsymbol{u}^T (\frac{1}{N}\sum_{n=1}^N \boldsymbol{x}_n \boldsymbol{x}_n^T) \boldsymbol{u} = \boldsymbol{u}^T (\frac{1}{N}\sum_{n=1}^N \boldsymbol{x}_n \boldsymbol{x}_n^T) \boldsymbol{u} = \boldsymbol{u}^T \boldsymbol{S} \boldsymbol{u}$
そして $\boldsymbol{S} \boldsymbol{u} = \lambda \boldsymbol{u}$ を使えば
$\boldsymbol{u}^T \boldsymbol{S} \boldsymbol{u} = \boldsymbol{u}^T \lambda \boldsymbol{u} = \lambda \boldsymbol{u}^T \boldsymbol{u} = \lambda$
よって、 $\frac{1}{N}\sum_{n=1}^N (\boldsymbol{u}^T \boldsymbol{x}_n)^2 = \lambda$ が導ける。

ところで、 $\boldsymbol{u}$ が満たす方程式

$\boldsymbol{S} \boldsymbol{u} = \lambda \boldsymbol{u}$
は、線形代数で言うところの、行列 $\boldsymbol{S}$ の固有方程式である。
これを満たす固有ベクトル $\boldsymbol{u}$ は、いくつもある。
$\lambda$ がそれぞれに対応する固有値である。

しかし、欲しかったのは、分散を最大化する $\boldsymbol{u}$ である。
$\lambda$ が分散 $\frac{1}{N}\sum_{n=1}^N (\boldsymbol{u}^T \boldsymbol{x}_n)^2$ に等しくなったのだから、
・・・ということは、最大の固有値に対応する固有ベクトルが、求めたかった $\boldsymbol{u}$ であることになる。

２．残差平方和を最小化する

$\boldsymbol{u}$ の上に、各ベクトル $\boldsymbol{x}_n$ を正射影すると、 $(\boldsymbol{u}^T \boldsymbol{x}_n) \boldsymbol{u}$ というベクトルを得ることはもう分かっている。
よって、差ベクトルは $\boldsymbol{x}_n - (\boldsymbol{u}^T \boldsymbol{x}_n) \boldsymbol{u}$ である。

この長さの平方和を最小化するような $\boldsymbol{u}$ を求めたい。つまり、

$\sum_{n=1}^N \| \boldsymbol{x}_n - (\boldsymbol{u}^T \boldsymbol{x}_n) \boldsymbol{u} \|^2$

を最小化する $\boldsymbol{u}$ を求めたい。

足されている $\| \boldsymbol{x}_n - (\boldsymbol{u}^T \boldsymbol{x}_n) \boldsymbol{u} \|^2$ を書き直す。

$\| \boldsymbol{x}_n - (\boldsymbol{u}^T \boldsymbol{x}_n) \boldsymbol{u} \|^2=\boldsymbol{x}_n^T\boldsymbol{x}_n-2(\boldsymbol{u}^T \boldsymbol{x}_n)^2+(\boldsymbol{u}^T \boldsymbol{x}_n)^2 \boldsymbol{u}^T\boldsymbol{u}=\boldsymbol{x}_n^T\boldsymbol{x}_n - (\boldsymbol{u}^T \boldsymbol{x}_n)^2$
書き直すとき、 $\boldsymbol{u}$ が単位ベクトルであることを使った。

$\boldsymbol{u}$ が何であれ、 $\boldsymbol{x}_n^T\boldsymbol{x}_n$ の部分は一定のままである。
ということは、解こうとしている最小化問題は

$- \sum_{n=1}^N (\boldsymbol{u}^T \boldsymbol{x}_n)^2$

の最小化と等価で、これは、先ほど最大化しようとしていた分散に $-N$ を掛けたものに過ぎない。
つまり、全く同じ問題を解いていることになる。
なので、答えも同じ。

というか、ピタゴラスの定理で斜辺の長さが一定の状況に相当するので、
残りの2辺のうち一方の長さの2乗を大きくすることは、
他方の長さの2乗を小さくすることと等価になる。

（おわり）